Alles was du über das Delta einer Option wissen musst
Zuletzt aktualisiert am 4. September 2024 von Tools-for-Trader
Das Delta $\Delta$ einer Option gehört zu den sogenannten Options-Griechen. Neben Gamma $\Gamma$ und Theta $\theta$ ist Delta, einer der wichtigsten mathematischen Kenngrößen einer Option, mit der wir als Optionstrader unser Portfolio managen. Alle oben genannten Griechen sind aus dem Black-Scholes Modell abgeleitet und beschreiben die wesentlichen Eigenschaften der Option bzw. des Optionsportfolios.
Inhalt
Was ist das Delta bei Optionen?
Das Delta $\Delta$ einer Option gibt an, wie sich der Optionspreis ändert, wenn sich der Basiswert um 1 USD (bzw. der Basiswährung) verändert. Mathematisch ausgedrückt handelt es sich bei dem Delta $\Delta$ also um die Ableitung des Optionspreises nach dem Preis des Basiswerts. Delta $\delta $ kann wie folgt als Formel ausgedrückt werden:
$$\Delta = \frac{\delta V}{\delta S} $$
Bei $\delta V$ handelt es sich um die Änderung des Optionspreises und bei $\delta S$ um die Änderung des Preises des Basiswerts.
Delta kann bei Optionen Werte zwischen +1 und -1 annehmen.
Delta der Call Option (Long und Short)
Eine Call-Option, mit einem Strikepreis über dem des Basiswerts, hat ein Delta $\Delta$ unter 0,5. Die Option liegt aus dem Geld. Je weiter die Option aus dem Geld liegt, desto geringer wird ihr Delta $\Delta$. Weit aus dem Geld liegende Call-Optionen haben letztendlich ein Delta $\Delta$ von 0 bzw. nahe 0.
Liegt der Strikepreis der Call-Option unter dem Preis des Basiswerts, ist das Delta $\Delta$ größer 0,5 und die Option ist im Geld. Je weiter die Option im Geld liegt, desto größer wird ihr Delta. Tief im Geld liegende Optionen haben ein Delta von 1 bzw. nahe 1.
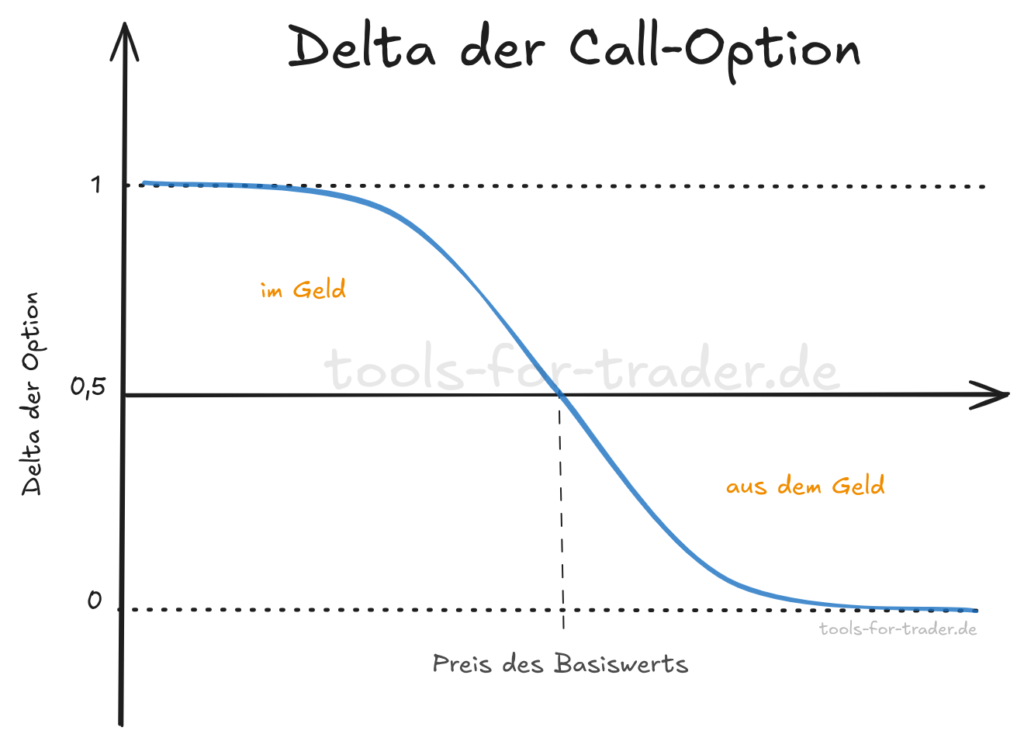
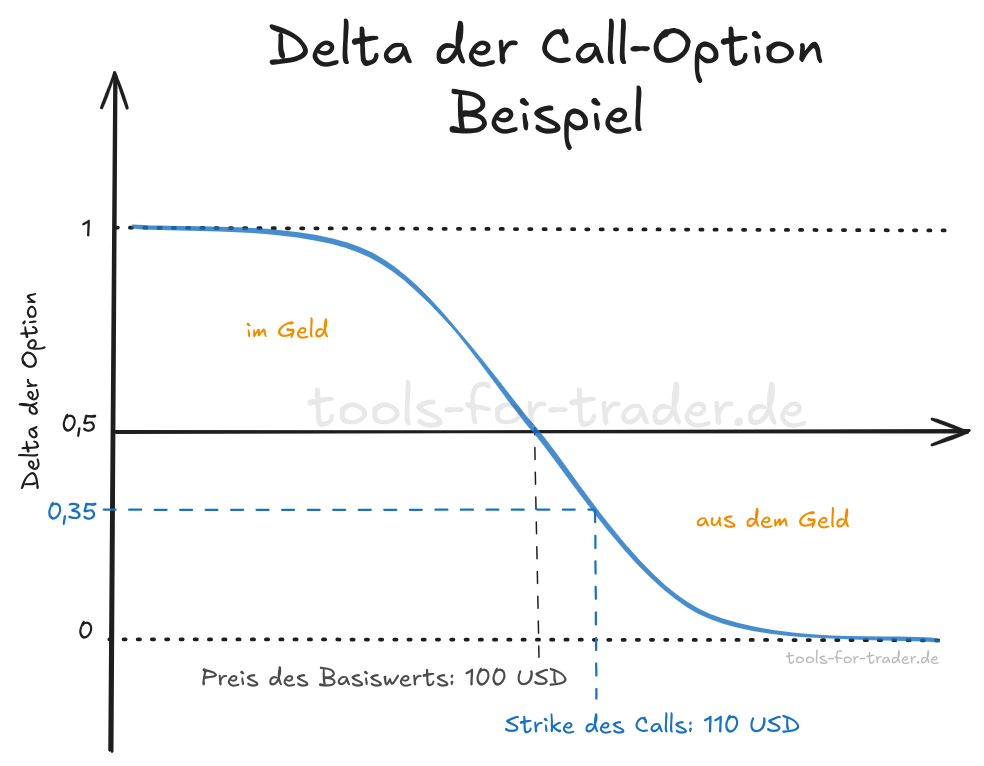
Das Delta von Long Call-Optionen kann somit zwischen 0 und 1 betragen. Mit der Long Call-Option positionieren wir uns bullisch und setzten auf einen steigenden Kurs des Basiswerts. Steigt der Basiswert im Preis, verdienen wir mit der Long Put-Option.
An dieser Stelle ein kurzes Zahlenbeispiel, wie wir den Call-Option Graph interpretieren können. Angenommen der Kurs des Basiswerts liegt bei 100 USD. In Abhängigkeit vom Strike des Basiswerts finden wir das Optionsdelta der Call-Option auf der blauen Linie. Liegt der Strike des Calls bei 110 USD, so beträgt das Delta des Calls diesem Beispiel bei ca. 0,35.
Positionieren wir uns als Short-Seller oder Stillhalter und verkaufen die Call-Option (Short) kehrt sich das Vorzeichen des Deltas um. Wir profitieren dann, wenn der Kurs des Basiswerts fällt bzw. der Kurs des Basiswerts unter dem Strikepreis der Option bleibt.Bei letzterem profitieren wir vom Theta der Option.
Zusammenfassung:
- Beim Long-Call beträgt das Delta zwischen 0 und 1 und wird umso größer, je tiefer die Option im Geld liegt.
- Die Call-Option liegt im Geld, wenn der Preis des Basiswerts über dem Strikepreis der Option liegt.
- Beim Short-Call kehrt sich das Vorzeichen des Deltas um.
Delta Put Option (Long und Short)
Eine Put-Option mit einem Strikepreis unter dem Preis des Basiswerts hat ein Delta $\Delta$ von größer -0,5. Die Option liegt hier aus dem Geld. Je weiter die Option aus dem Geld liegt, desto näher liegt ihr Delta $\Delta$ an 0. Weit aus dem Geld liegende Put-Optionen haben letztendlich ein Delta $\Delta$ von 0 bzw. nahe 0.
Liegt der Strikepreis der Put-Option über dem Preis des Basiswerts, ist das Delta $\Delta$ kleiner -0,5. und die Option ist im Geld. Je weiter die Put-Option im Geld liegt, desto kleiner wird ihr Delta. Tief im Geld liegende Optionen haben ein Delta von -1 bzw. nahe -1.
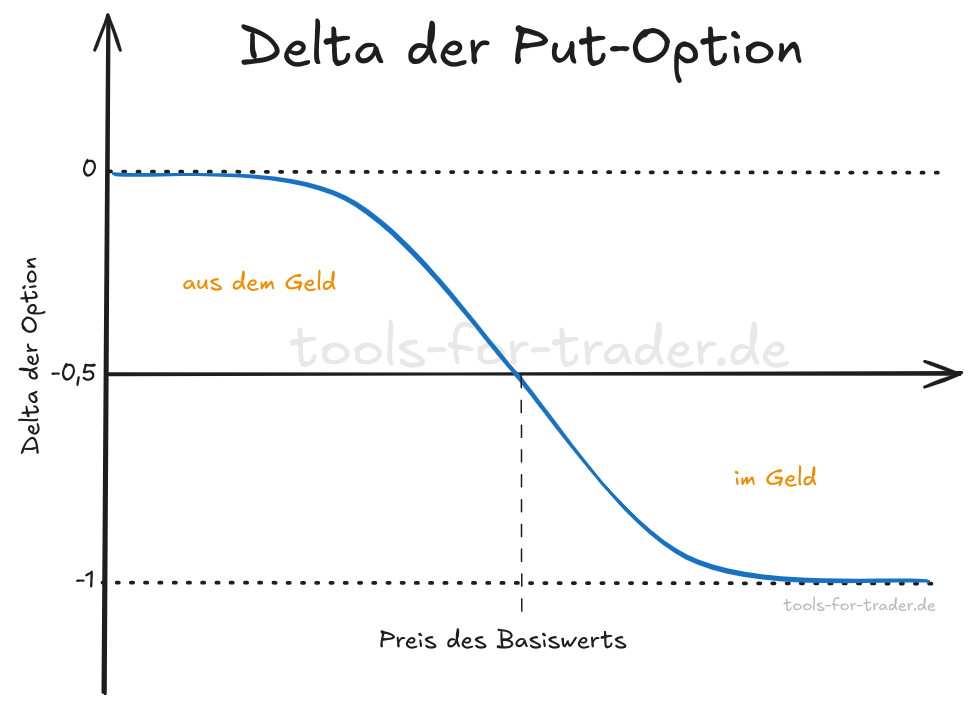
Das Delta von Long Put-Optionen kann somit zwischen 0 und -1 betragen. Mit der Long Put-Option positionieren wir uns bärisch und setzten auf einen fallenden Kurs des Basiswerts. Fällt der Basiswert im Preis, verdienen wir mit der Long Put-Option.
Hier ein kurzes Zahlenbeispiel, wie wir den Put-Optionen Graph interpretieren. Angenommen der Kurs des Basiswerts liegt bei 100 USD. In Abhängigkeit vom Strike des Basiswerts finden wir das Optionsdelta der Put-Option dann auf der blauen Linie. Liegt der Strike des Puts bei 90 USD, so ist das Delta in diesem Beispiel bei ca. -0,16.
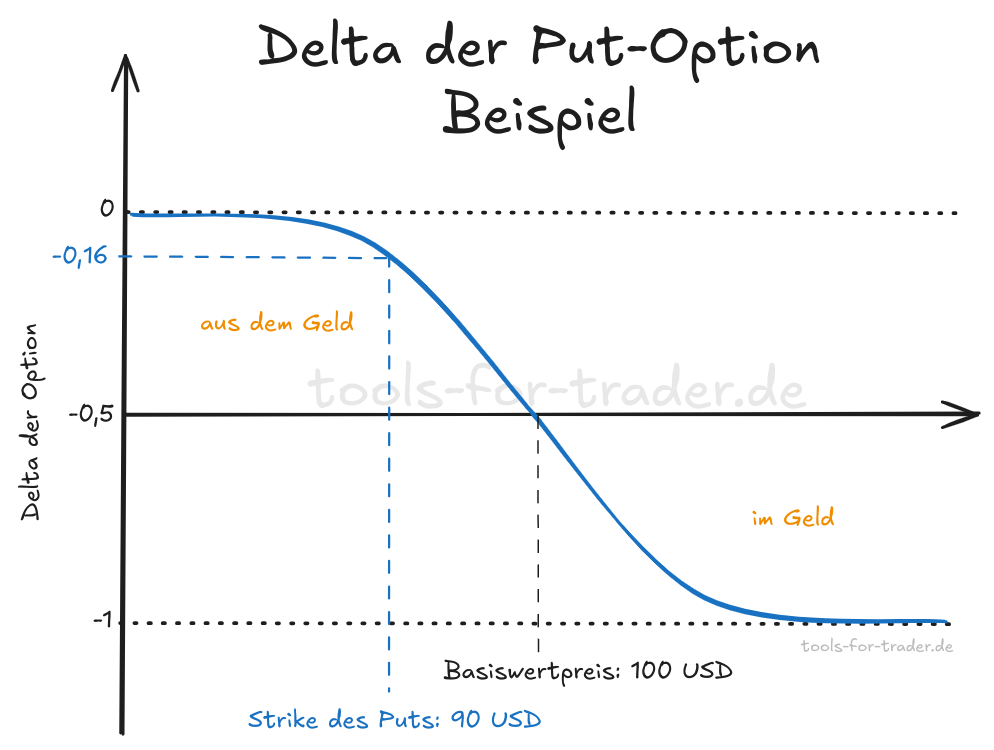
Positionieren wir uns auf der anderen Seite des Trades, nämlich als Short-Seller der Option oder Stillhalter und verkaufen die Call-Option (Short bzw. Schreiben der Option), kehrt sich das Vorzeichen des Deltas $\Delta$ um. Wir profitieren dann, wenn der Kurs des Basiswerts steigt bzw. der Kurs des Basiswerts über dem Strikepreis der Option bleibt. Bei letzterem profitieren wir vom Theta der Option.
Zusammenfassung:
- Beim Long-Put beträgt das Delta zwischen 0 und -1 und wird umso kleiner, je tiefer die Option im Geld liegt.
- Die Put-Option liegt im Geld, wenn der Preis des Basiswerts unter dem Strikepreis der Option liegt.
- Beim Short-Put kehrt sich das Vorzeichen des Deltas um.
Zahlenbeispiel für das Options-Delta
Schauen wir uns zwei konkrete Beispiele für das Delta der Put-Option an.
Long Put auf Tesla
Angenommen wir kaufen eine Option auf Tesla (TSLA) mit einem Delta $\Delta$ von -0,2, da wir darauf spekulieren, dass der Kurs der Tesla Aktie im Wert fällt. Der Kurs von Tesla beträgt zu diesem Zeitpunkt 218 USD.
Wir erinnern uns oben an die Definition von Delta und stellen die Gleichung nach $\delta V$ um:
$$\delta V = \Delta* \delta S$$
Bei $\delta V$ handelt es sich um die Änderung des Optionspreises und bei $\delta S$ um die Änderung des Preises des Basiswerts.
Besitzen wir nun diese Option und sind long, so verhält sich der Gewinn und Verlust wie folgt:
- Mit jedem USD den Tesla im Wert steigt, verliert unsere Option 0,2 USD im Wert
- Mit jedem USD den Tesla im Wert fällt, gewinnt unsere Option 0,2 USD im Wert
Diese Rechnung ist eine Momentaufnahme, da sich mit der Änderung Basiswertkurses und den Tagen bis zum Verfall auch das Gamma der Option stetig ändert.
Short Put auf Tesla
Nun platzieren wir uns auf der Short Seite des Trades und als Stillhalter. Wir setzen darauf, dass Tesla entweder steigt oder zumindest nicht tiefer fällt als der Strike der Option.
Angenommen, wir verkaufen dieselbe Option auf Tesla (TSLA). Für uns hat diese jetzt aber ein positives Delta $\Delta$ von +0,2, da wir short sind.
Die Gewinn- und Verlustrechnung kehrt sich damit um:
- Mit jedem USD den Tesla im Wert steigt, gewinnt auch unsere Optionsposition 0,2 USD im Wert.
- Mit jedem USD den Tesla im Wert fällt, verliert auch unsere Optionsposition 0,2 USD im Wert.
Hinzukommt kommt bei verkauften Optionen, dass wir vom Zeitwertverfall [[Theta]] profitieren. Bleiben alle Parameter gleich, verdienen wir damit täglich Geld.
Bei dieser Rechnung handelt es sich auch wieder nur um eine Momentaufnahme, da sich mit der Änderung des Preises des Basiswerts und den Tagen bis zum Verfall auch das Gamma der Option stetig ändert.
Delta bei unterschiedlichen Optionslaufzeiten (DTE)
Das Delta $\Delta$ der Option (DTE: Days to Expiration) verändert sich mit der Laufzeit der Option.
Dies liegt im Wesentlichen daran, dass der Markt die Schwankungsbreite (Volatilität) zukünftiger Kurse einpreist. Je länger der Betrachtungszeitraum ist, desto höher ist auch die mögliche Schwankungsbreite und damit die erwartete Volatilität (implizite Volatilität).
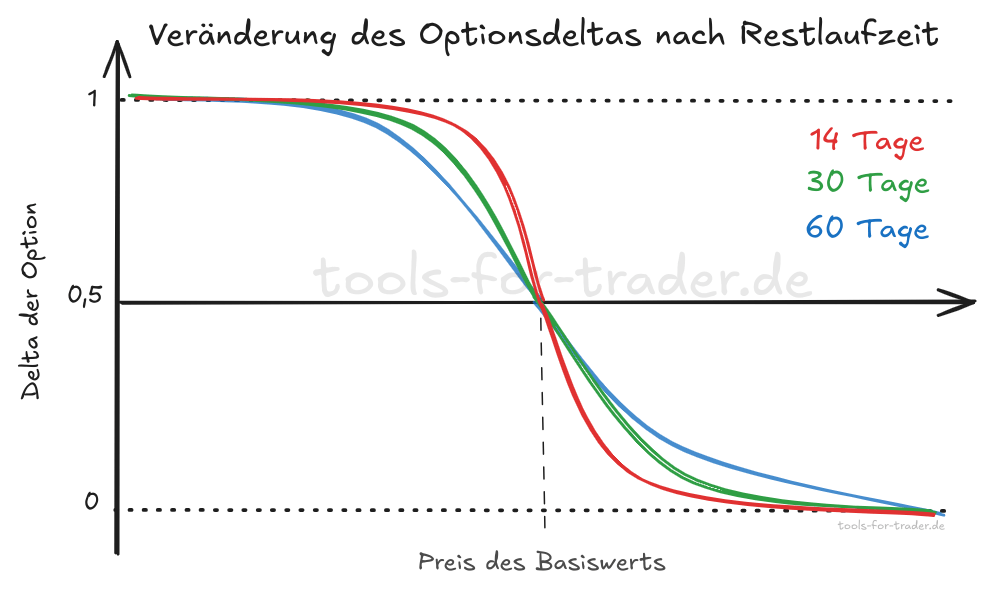
Dies führt dazu, dass die Optionsdeltas breiter über mehr Kurse des Basiswerts gestreut sind, um so länger die Restlaufzeit der Option. Die Kurve des Deltas auf dem Chart wird flacher.
Wird die Zeit bis zum Verfall der Option kürzer, so preist der Markt geringere Schwankungsbreiten der Preise ein und die Kurve wird steiler. Aus Sicht des Marktes wird dann ein immer enger werdendes Fenster an zukünftigen Kursen möglich, je kürzer die Laufzeit.
Bei der Steigung (1. Ableitung) des Deltas im Graphen handelt es sich um Gamma, einen weiteren Optionsgriechen und damit um die Änderung des Deltas bei Veränderung des Basiswerts. Gamma ist auch der Grund, wieso Stillhalter kurze Optionslaufzeiten vermeiden sollten.
Delta bei unterschiedlicher Volatilität
Bei Änderung der Volatilität verhält sich Delta ähnlich, wie bei unterschiedlichen Laufzeiten der Option ([[Delta bei unterschiedlichen Optionslaufzeiten (DTE)]]).
Unter normalen Umständen, d.h. wenn sich der Markt im Contango befindet, nimmt die implizite Volatilität (zukünftige Volatilität) zu, je länger der Betrachtungszeitraum ist. Daher sind die Deltas bei längeren Optionslaufzeiten über eine größere Anzahl von Preisen verteilt und die Wahrscheinlichkeiten für breite Preissprünge eingepreist.
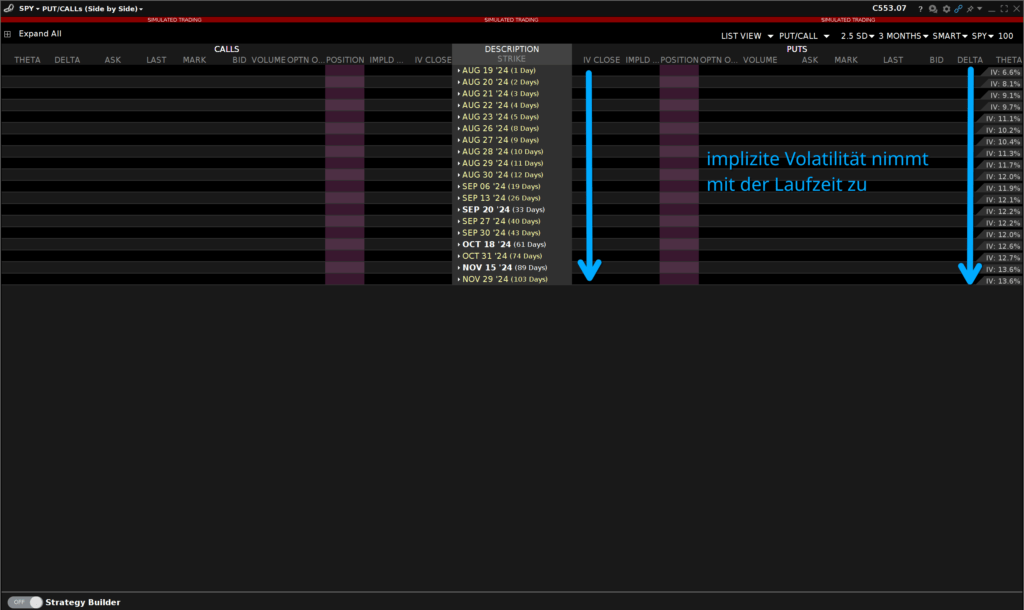
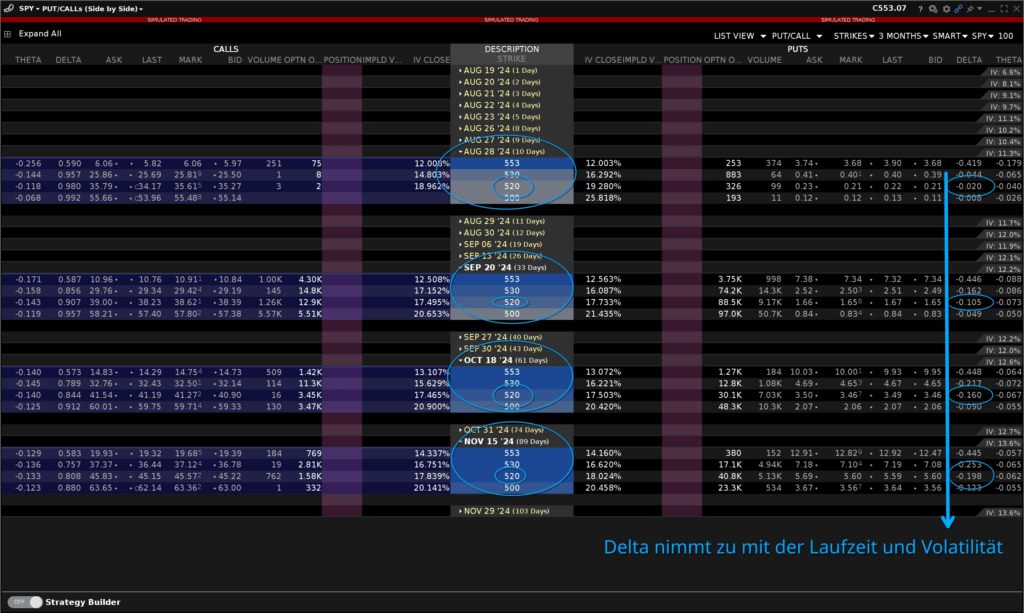
Ein Blick in die Optionskette des SPY in der Trader Workstation von Interactive Brokers zeigt die Verteilung von Delta über verschiedene Laufzeiten und die implizite Volatilität dieser Laufzeiten.
Schauen wir uns nun unterschiedliche Laufzeiten im Detail an, so sehen wir wie für den selben Strike von 520 USD, dass das Delta mit längerer Optionslaufzeit größer wird. Der Markt hält es um so wahrscheinlicher, dass SPY diesen Preis erreicht. Und zwar je länger wir in die Zukunft schauen.
Das Delta beim Optionshandel in der Praxis
Das Delta der Option kann beim Optionshandel für unterschiedliche Anwendungsfälle genutzt werden. Hier einige der häufigsten.
Richtungsabhängigkeit des Trades
Wie wir im Beispiel gesehen haben, ist Delta die Kenngröße bei Optionen, die die Richtungsabhängigkeit der Option zum Basiswert widerspiegelt. Bei einem Delta von 0,2 bewegt sich der Kurs der Option mit dem 0,2-fachen des Basiswertes. Wollen wir mit der Option 50 % der Preisbewegung des Basiswerts replizieren, so könnten wir eine Option mit einem Delta $\Delta$ von 0,5 kaufen. Wollen wir genau die entgegengesetzte Bewegung abbilden, so kaufen wir beispielsweise Puts (mit negativem Delta) oder verkaufen Calls.
Hedging und Absicherung
Angenommen, wir haben 100 Tesla Aktien (TSLA) in unserem Portfolio. In Delta ausgedrückt entsprechen 100 Long Aktien einem Delta $\Delta$ von 1.
Wollten wir nun unseren Anteil an der Preisbewegung der Teslaaktie verringern, gleichzeitig aber alle Aktien im Portfolio behalten, können wir die Position mit zusätzlichem Short Delta hedgen. Wir kaufen dazu beispielsweise eine Put-Option mit einem Delta von -0,15. Damit reduzieren wir dann das Portfolio-Delta der Position um 0,15. Unsere TSLA Position weist dann nur noch ein Delta von 0,85 auf und bildet damit 85 % der Preisbewegung von Tesla nach oben und nach unten ab.
Delta-Hedging ist für Optionshändler das Tagesgeschäft und führt zu weniger Volatilität im Portfolio bei geringerem Risiko.
Wahrscheinlichkeit, mit der die Option im Geld verfällt
Als [[Stillhalter]] wollen wir mit dem Verkauf von Optionen Cashflow generieren. Daher möchten wir möglichst Optionen verkaufen, die eine hohe Gewinnwahrscheinlichkeit (PoP) haben. Eine Möglichkeit, dies schon vor dem Trade abzuschätzen, ist ein Blick auf das Delta der Option. Eine Put-Option einem Delta von 0,16 verfällt zu ca. 84 % (Berechnung: 1 – 0,16) wertlos. Das Options-Delta hilft also Stillhaltern, die passenden Optionen für die Stillhalterstrategie auszuwählen.