Zuletzt aktualisiert am 6. Juni 2023 von Tools-for-Trader
In diesem Beitrag wollen wir zunächst klären, was Korrelation grundsätzlich bedeutet. Wir erläutern die Bedeutung der Korrelation für Trader und Investoren im Allgemeinen. Danach schauen wir uns an, wie Korrelation berechnet und in einer Korrelationsmatrix dargestellt werden kann und klären die Bedeutung der Korrelationskoeffizienten. Am Schluss geht es dann noch um die eigentliche Berechnung der Korrelation.
Am Ende des Beitrags findest du eine Korrelationsmatrix der wichtigsten ETFs, die unterschiedlichste Anlagen replizieren. Diese Korrelationsmatrix wird täglich aktualisiert. Falls du also auf der Suche nach der aktuellen Korrelation der häufigsten ETFs über jeweils 3 Monate, 6 Monate und einem Jahr bist, dann bist du hier genau richtig.
Inhalt
Was bedeutet Korrelation?
Das Konzept der Korrelation beschreibt das Ausmaß, in dem zwei oder mehr Variablen dazu neigen, sich synchron zu bewegen. Bei börsengehandelten Fonds (ETFs) gibt die Korrelation an, wie sich der Kurs eines ETFs im Verhältnis zu einem anderen verhält.
Angenommen, die Kurse zweier ETFs steigen oder sinken häufig gleichzeitig, dann spricht man von einer positiven Korrelation. Steigt der Kurs des einen ETF, wenn der des anderen sinkt, haben sie eine negative Korrelation. Wenn du die Bedeutung der Korrelation verstehst, kannst du künftige ein gut diversifiziertes Anlageportfolio aufbauen und so auch das Ausmaß der Volatilität in deinem gesamten Anlageportfolio reduzieren.
Die Bedeutung von Korrelation für Trader und Investoren
Für Trader und Investoren ist das Verständnis der Korrelation wichtig. Es hilft dabei, eine wirksame Diversifizierungsstrategie zu entwickeln und die gegenseitigen Abhängigkeiten der Investitionen in einem Anlageportfolio zu bewerten.
Wenn die ETFs in deinem Portfolio alle positiv korreliert sind, können sie bei einem Markteinbruch gemeinsam an Wert verlieren, was das Risiko von hohen Verlusten erhöht. Im Gegensatz dazu kann die Aufnahme von ETFs, die negativ korreliert sind oder keine Korrelation aufweisen, die Auswirkungen von Marktschwankungen ausgleichen und so die Widerstandsfähigkeit deines Portfolios verbessern.
Der Korrelationskoeffizienz
Der Grad der Korrelation wird mit einem Korrelationskoeffizienten quantifiziert. Dieser kann Werte zwischen -1 und +1 annehmen. Ein Koeffizient von +1 steht für eine perfekte positive Korrelation, was bedeutet, dass sich die ETFs gemeinsam in die gleiche Richtung bewegen. Ein Koeffizient von -1 steht für eine perfekte negative Korrelation, d.h. die ETFs bewegen sich in entgegengesetzter Richtung. Und ein Koeffizient von 0 zeigt an, dass es keine Korrelation gibt, was bedeutet, dass die Bewegungen der ETFs unabhängig voneinander sind.
Oder anders ausgedrückt:
Eine positive Korrelation entsteht, wenn sich zwei ETFs in die gleiche Richtung entwickeln, z. B. zwei ETFs, die den gleichen Index abbilden.
Eine negative Korrelation tritt auf, wenn zwei ETFs in entgegengesetzte Richtungen tendieren. Ein Beispiel wäre ein ETF, der einen Aktienindex abbildet, und ein anderer, der einen Rentenindex abbildet.
Wenn ETF 1 und ETF 2 zum Beispiel einen Korrelationskoeffizienten von 0,8 haben, bedeutet dies eine starke positive Korrelation. Wenn also der Preis von ETF 1 steigt, steigt auch der Preis von ETF 2 tendenziell.
Die Korrelationsmatrix
Eine Korrelationsmatrix ist eine tabellarische Darstellung der Korrelationskoeffizienten zwischen mehreren ETFs. Sie liefert eine Momentaufnahme der Beziehungen zwischen den ETFs. Positive Korrelationen werden hier grün, negative Korrelationen rot und keine Korrelation grau dargestellt.
Angenommen, du hast eine Matrix mit ETF 1 und ETF 2. Wenn die Korrelation zwischen ETF 1 und ETF 2 0,7 beträgt, bedeutet das eine hohe positive Korrelation. Wenn die Korrelation zwischen ETF 1 und ETF 2 -0,5 beträgt, deutet dies auf eine mäßige negative Korrelation hin. Aber wenn die Korrelation zwischen ETF 1 und ETF 2 nahe bei 0 liegt, bedeutet das, dass keine Korrelation besteht.
In diesem Blogbeitrag findest du die Korrelationsmatrix für die wichtigsten US ETFs weiter unten auf dieser Seite. Diese werden einmal pro Tag aktualisiert.
Wie du die Korrelation zwischen zwei ETFs berechnest
Im Folgenden findest du eine allgemeine Anleitung zur Berechnung der Korrelation zwischen zwei ETFs auf Basis der Tagesschlusskurse. Wir werden an dieser Stelle nicht jede Formel bis ins Detail erklären. Viel mehr soll dies eine Übersicht der einzelnen Schritte liefern.
Schritt 1: Sammle die Daten
Sammle oder downloade historische Kursdaten für die beiden ETFs, die dich interessieren. Welchen Zeitraum du wählst, hängt von deinem Handels- oder Investitionszeitraum ab. Du kannst tägliche Schlusskurse verwenden, wenn du eine kurzfristige Korrelation suchst, oder monatliche Schlusskurse für eine langfristige Analyse. Diese Daten findest du in der Regel auf Finanzwebseiten oder -plattformen.
Schritt 2: Berechne die Renditen
Die Korrelation wird normalerweise anhand der Renditen und nicht anhand der Preise berechnet. Um die Rendite zu berechnen, verwendest du die folgende Formel
Tagesrendite = (Schlusskurs_heute - Schlusskurs_gestern) / Schlusskurs_gesternFühre dies für beide ETFs für jeden Zeitraum in deinem Datensatz durch.
Schritt 3: Berechne die mittlere Rendite
Berechne den Durchschnitt dieser Renditen für jeden ETF, indem du die Summe aller berechneten Renditen durch die Anzahl der Tage teilst.
Schritt 4: Berechne die Varianz
Ermittle für jeden ETF die Varianz der Renditen. Die Varianz wird als Durchschnitt der quadrierten Differenzen zum Mittelwert berechnet.
Schritt 5: Berechne die Kovarianz
Die Kovarianz misst, wie stark sich zwei Variablen zusammen bewegen. Sie wird als Durchschnitt des Produkts aus den Differenzen der Renditen der einzelnen ETFs zu ihren jeweiligen Mittelwerten berechnet.
Schritt 6: Berechne die Standardabweichung
Berechne die Standardabweichung für jeden ETF.
Schritt 7: Berechne den Korrelationskoeffizienten
Schließlich wird der Korrelationskoeffizient als Kovarianz / (Standardabweichung ETF1 * Standardabweichung ETF2) berechnet.
Mit dieser Herangehensweise erhältst du einen Korrelationskoeffizienten zwischen -1 und 1. Liegt der Koeffizient nahe bei 1, haben die ETFs eine starke positive Korrelation (sie bewegen sich im Allgemeinen in dieselbe Richtung). Liegt er nahe bei -1, haben sie eine starke negative Korrelation (sie bewegen sich in der Regel in die entgegengesetzte Richtung). Wenn der Wert nahe bei 0 liegt, gibt es keine signifikante Korrelation zwischen den Bewegungen der ETFs.
Bevor du dir aber die Mühe machst, selber die Berechnung vorzunehmen, nutze gerne die Korrelationsmatrizen auf dieser Seite.
Fazit und Kurzfassung
Die Korrelation von zwei ETFs zeigt auf, wie diese sich im Verhältnis zueinander bewegen. Dabei stellt der Korrelationskoeffizienz von +1 dar, dass diese ETFs sich genau gleich bewegen. -1 bedeutet, dass diese sich genau entgegengesetzt bewegen und ein Koeffizient von 0 sagt aus, dass diese nicht korreliert sind. Die Korrelation lässt sich als Korrelationsmatrix (siehe unten) darstellen und bietet so eine Übersicht, zu der Korrelation von vielen ETFs untereinander. Mithilfe der Korrelation lässt sich ein diversifiziertes Anlageportfolio aufbauen und somit Portfolioschwankungen reduzieren.
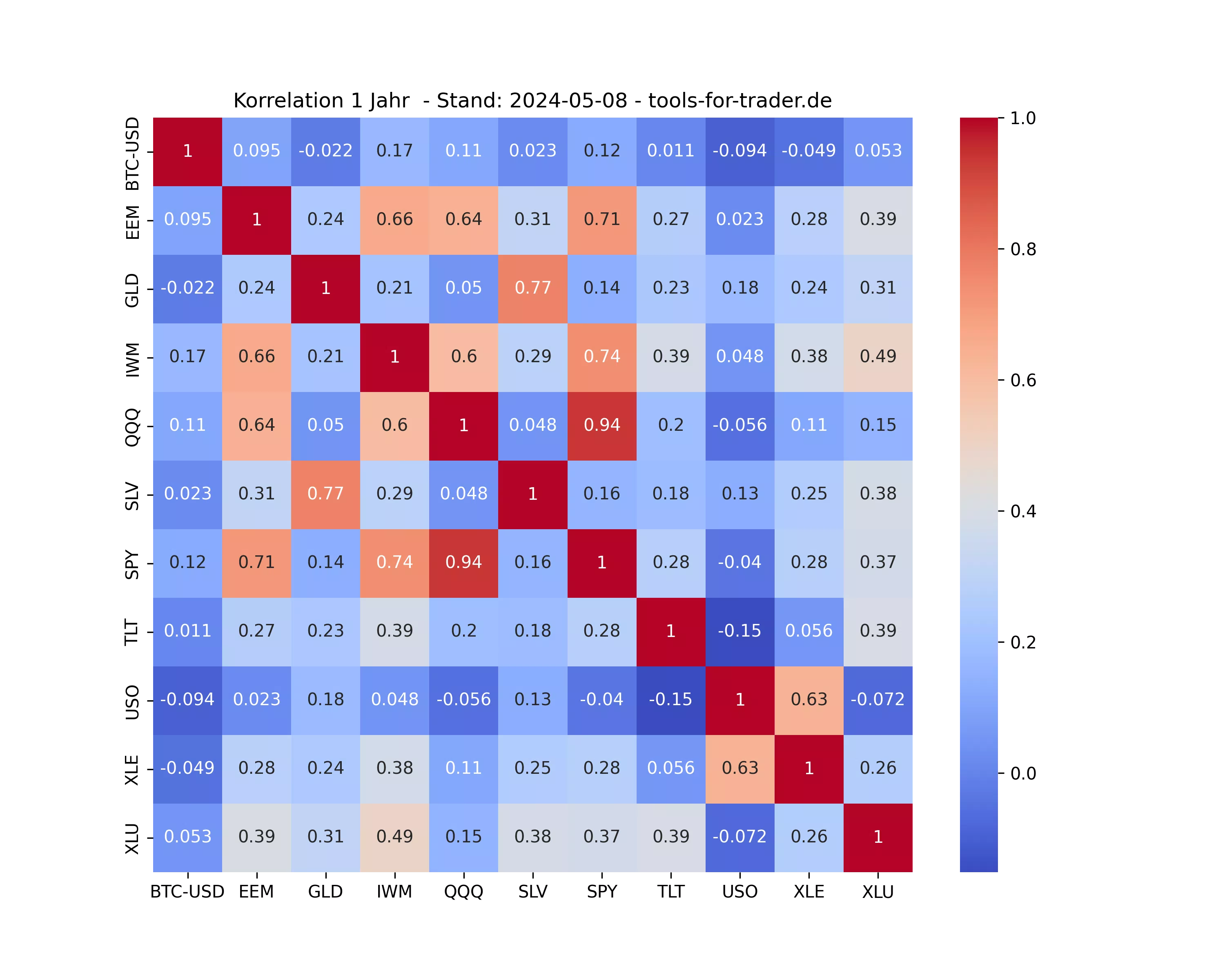
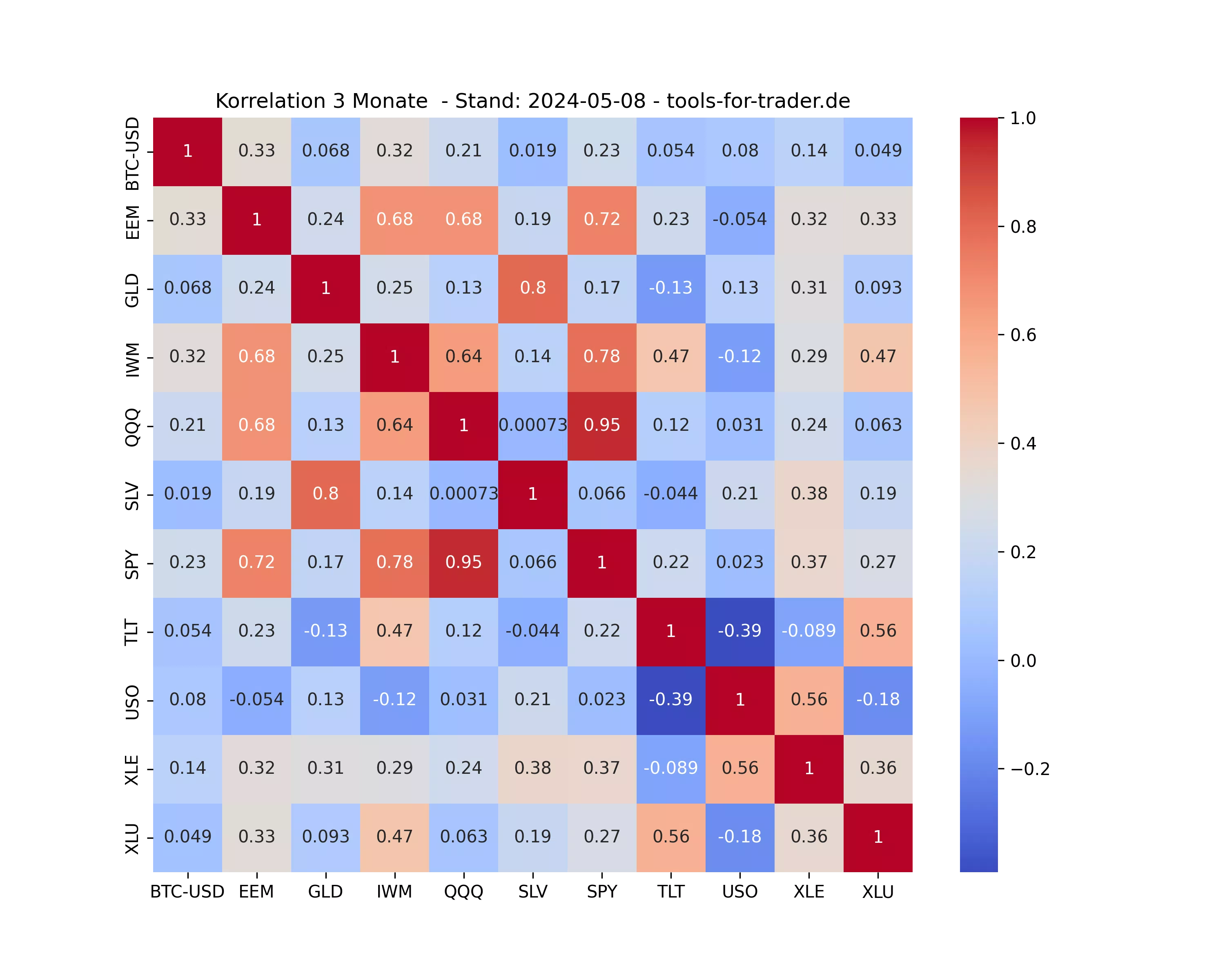
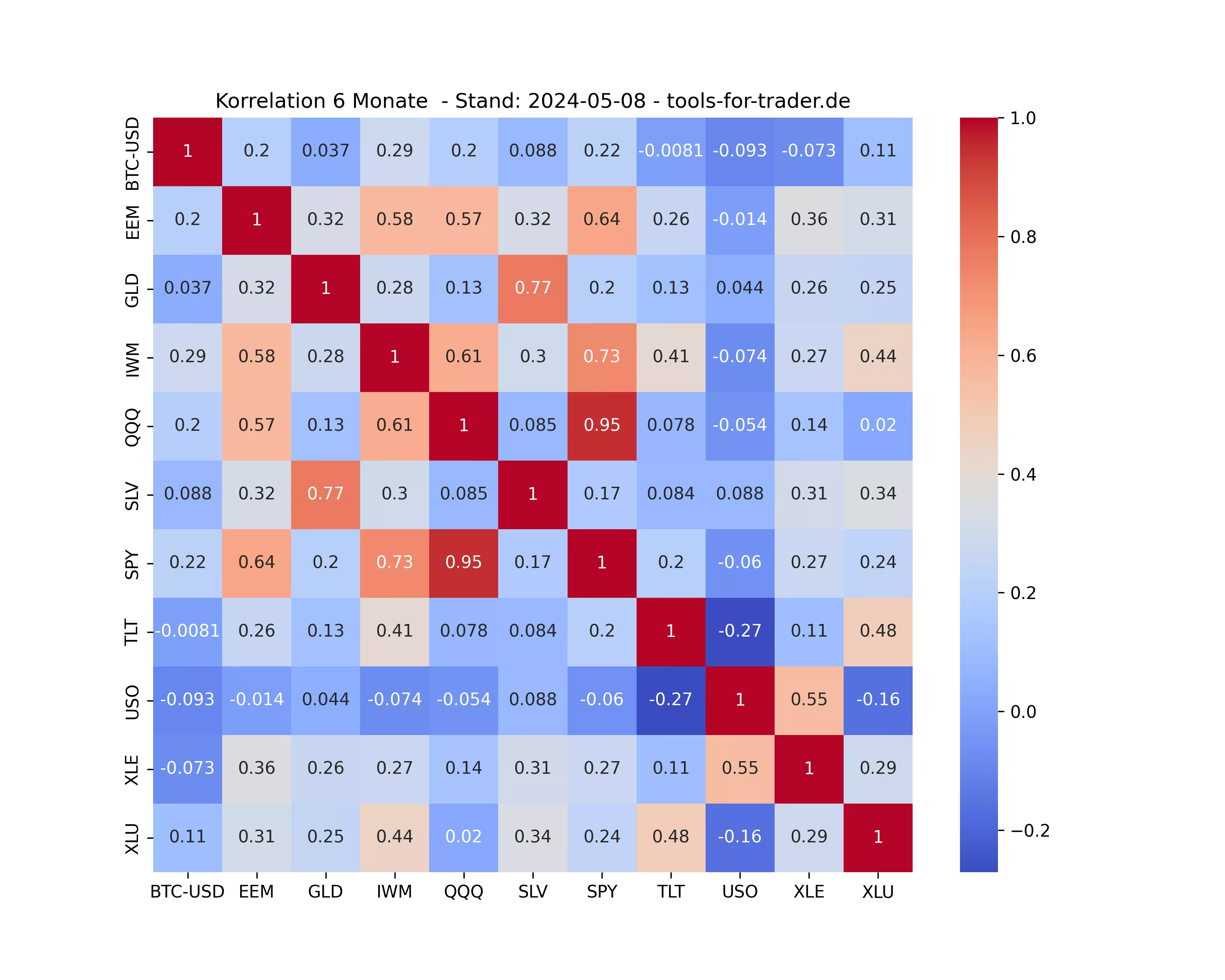
Zum Schluss findest du hier folgend die Korrelationsmatrizen der wichtigsten US ETFs.
Korrelation der wichtigsten ETFs – Täglich aktualisiert
Im Folgenden findest du die Korrelationsmatrizen für die wichtigsten und meist gehandelten US ETFs.
Diese werden einmal pro Tag hier aktualisiert.
3 Monats-Korrelation der ETFs
6 Monats-Korrelation der ETFs
1 Jahres-Korrelation der ETFs