Zuletzt aktualisiert am 16. Juni 2023 von Tools-for-Trader
Als Teilnehmer am Aktienmarkt ist das Management von Risiken eines der wichtigsten Punkte überhaupt, um zu überleben. Daher erläutern wir in diesem Artikel das Konzept des Value at Risk (VaR), einer statistischen Kennzahl, die die potenziellen Verluste einer Investition quantifiziert. Wir erklären dir, wie VaR funktioniert, wie er berechnet wird und erläutern ein praktisches Beispiel Anhand des SPY ETFs. Den ETF auf den S&P 500. Am Ende dieses Artikels wirst du ein solides Verständnis des VaR haben, um ein besseres Verständnis für das Risiko zu haben, welches in deinem Portfolio schlummert.
Fangen wir damit an, was Value at Risk (VaR) überhaupt bedeutet.
Inhalt
Was bedeutet Value at Risk (VaR)?
Hast du dich schon einmal gefragt, wie viel Risiko in deiner Investition oder in deinem Porfolio für einen bestimmten Zeitraum steckt?
Genau hier kommt der VaR ins Spiel. Der Value at Risk (VaR) ist eine statistische Methode aus der Finanzmathematik, um die Verlustgrenze in deinem Portfolio zu schätzen, die mit einer festgelegten Wahrscheinlichkeit, unter normalen Marktbedingungen und über einen bestimmten Zeitraum, auftritt. Es ist eine beliebte Methode in der Finanzbranche, um das Risiko eines Portfolios quantitativ darzustellen.
Diese Quantifizierung des Risikos ermöglicht es dir, dein Portfolio effektiver zu managen und Risiko und Ertrag entsprechend deiner Risikobereitschaft abzuwägen.
VaR und das Konfidenzlevel
Im Kern misst der VaR den mindestens zu erwarteten Verlust über einen bestimmten Zeitraum bei einem bestimmten Konfidenzlevel und unter normalen Marktbedingungen.
Im Zusammenhang mit dem VaR stellt das Konfidenzlevel die Wahrscheinlichkeit dar, dass ein bestimmtes Verlustniveau innerhalb eines bestimmten Zeitrahmens nicht überschritten wird. Es ist ein entscheidendes Element bei der VaR-Berechnung, da es die Grenze für die erwarteten Verluste festlegt.
Ein Beispiel:
Wenn wir einen VaR von 1 Mio. USD bei einem Konfidenzlevel von 95 % angeben, bedeutet dies, dass die Wahrscheinlichkeit, dass die Verluste innerhalb des angegebenen Zeitraums 1 Mio. USD übersteigen, nur 5 % beträgt. Mit anderen Worten: Wir sind zu 95 % sicher, dass der Verlust nicht mehr als 1 Mio. $ betragen wird.
In der Praxis wird bei VaR-Berechnungen häufig ein Konfidenzlevel von 99 % verwendet. Bei der Wahl des Konfidenzlevels geht es jedoch oft um ein Gleichgewicht zwischen Präzision und Praktikabilität. Ein höheres Konfidenzlevel führt zu einer konservativeren Schätzung des Risikos, geht aber auf Kosten der Präzision, da es weniger wahrscheinliche Extremereignisse berücksichtigt. Daher hängt die Wahl eines geeigneten Konfidenzlevels weitgehend von der Person ab, die das Portfolio managt.
Berechnung des Value at Risk (VaR)
Es gibt verschiedene Methoden, um den VaR zu berechnen, jede mit ihren Vor- und Nachteilen. Schauen wir uns drei der beliebtesten Methoden an:
- Die Varianz-Kovarianz-Methode
- Die historische Simulation
- Die Monte-Carlo-Simulation.
Varianz-Kovarianz-Methode
Bei der Varianz-Kovarianz-Methode wird der VaR unter der Annahme berechnet, dass die Portfolioerträge normal verteilt sind. Sie verwendet die Standardabweichung (oder Volatilität) der Portfoliorenditen und einen Z-Score, der die Anzahl der Standardabweichungen eines Elements vom Mittelwert angibt, um die potenziellen Verluste zu berechnen.
Z-Score = (Beobachtung - Mittelwert) / StandardabweichungDiese Methode wird aufgrund ihrer Einfachheit häufig verwendet. Ihr größtes Manko ist jedoch, dass sie eine Normalverteilung voraussetzt, die in der Realität nicht unbedingt zutrifft. Wenn die Standardabweichung der Portfoliorenditen beispielsweise 2 % beträgt und der Z-Score für ein Konfidenzlevel von 95 % bei 1,645 liegt, würde der Ein-Tages-VaR 2 %*1,645 = 3,29 % betragen. Das bedeutet, dass die Wahrscheinlichkeit, dass das Portfolio an einem Tag mehr als 3,29 % seines Wertes verliert, 5 % beträgt.
Historische Simulation
Bei der historischen Simulation wird der VaR anhand historischer Renditedaten berechnet, um eine empirische Verteilung zu erstellen. Der VaR wird dann aus dieser Verteilung mit dem gewählten Konfidenzlevel abgeleitet. Anders als bei der Varianz-Kovarianz-Methode wird hier nicht von einer Normalverteilung ausgegangen, sodass die in den historischen Daten vorhandenen Schräglagen (Skew) und Wölbungen (Kurtosis) erfasst werden. Ihr größter Nachteil ist, dass sie davon ausgeht, dass sich die Geschichte wiederholt. Dies ist natürlich nicht immer der Fall.
Monte-Carlo-Simulation
Die Monte-Carlo-Simulation ist eine komplexere, aber auch flexiblere Methode. Dabei wird eine große Anzahl möglicher Ergebnisse (zum Beispiel Kursverläufe einer Aktie) für einen bestimmten Satz von Risikofaktoren generiert und eine Wahrscheinlichkeitsverteilung erstellt. Aus dieser wird dann der VaR berechnet wird. Sie ist nicht auf eine bestimmte Verteilung oder historische Daten angewiesen, was sie anpassungsfähiger macht. Allerdings in die Monte-Carlo-Simulation aufwändiger und hängt von der Genauigkeit der verwendeten Modelle für das Finanzinstrument ab.
Die Berechnungsschritte des VaR mit Monte-Carlo Simulation
Um den VaR zu berechnen, sind folgende Schritte im Detail notwendig:
- Bestimme ein Konfidenzlevel für die Berechnungen (z.B. 95 %).
- Bestimme den Zeitraum, für den du den CVaR berechnen möchtest (z.B. ganze Handelstage)
- Führe eine Monte-Carlo Simulation der Schlusskurse z.B. auf Basis der historischen Volatilität der Anlage durch, für die der VaR berechnet werden soll (z.B. SPY oder dein Portfolio).
- Berechne die log-Returns auf Basis dieser Schlusskurse.
- Bestimmte die Grenze in der Verteilung log-Returns, welche die höchsten1 % aller Verluste umfasst.
Value at Risk (VaR) in der Praxis
Das Konzept von Value at Risk hilft dir ein Verständnis für mögliche Verluste zu erzeugen, die am Rande der gewöhnlichen Renditeverteilung einer Anlage liegen. Die umfasst auch Tail-Risk Verluste. Das heißt, Verluste am Rande der Wahrscheinlichkeitsverteilung.
Zur Veranschaulichung schauen wir uns die Wahrscheinlichkeit des täglichen Returns des SPY ETF an. Das Plot beinhaltet die historischen Returns des SPY ETF der letzten 10 Jahre.
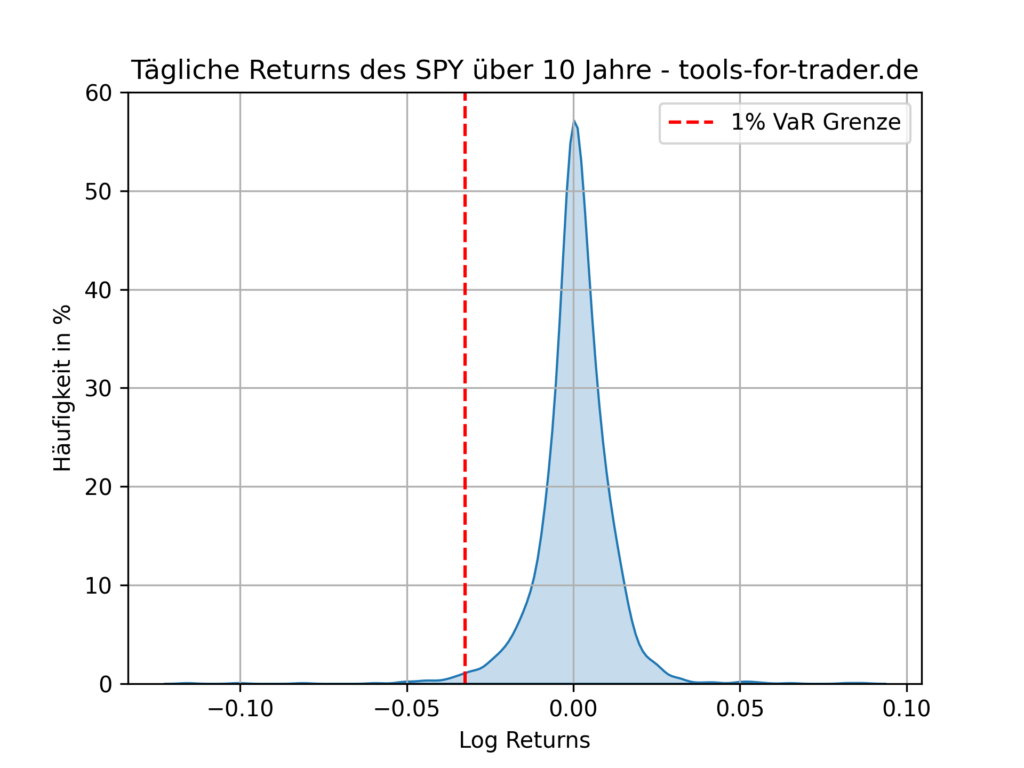
Gehen wir von einem Konfidenzlevel von 99 % aus, so interessiert uns die Grenze der Verluste, die maximal in 1 % der Fälle auftreten können. Oder anders ausgedrückt: Wir wollen wissen, welche Verluste an 99 % % der Handelstage der letzte 10 Jahre nicht überschritten werden.
Wir erkennen an der Wahrscheinlichkeitsverteilung, dass die Spitze der Verteilung leicht nach rechts geneigt ist. Dies ergibt hier ja auch Sinn, da der SPY im Schnitt 7-8 % Rendite pro Jahr abgeworfen hat. Da die Fläche unter der Wahrscheinlichkeitsverteilung immer 1 ergeben muss, muss die Kurve am linken Rand (Tail) Ausreißer (Outlier) aufweisen. Für dieses Beispiel liegt die 1 % Grenze bei -0.03248. Dies bedeutet, dass an 1 % der Tage Tagesverluste von 3,248 % oder größer aufgetreten sind.
Value at Risk Berechnung in der Handelsplattform (Trader Workstation)
Die Trader Workstation (TWS) von Interactive Brokers beinhaltet bereits einen Risk Navigator. Hier besteht die Möglichkeit Value At Risk (VaR) für das eigene Portfolio direkt aus der Handelsplattform heraus zu berechnen. Dazu bietet die TWS hier zwei Berechnungsmöglichkeiten. Die Simulation auf Basis der historischen Daten und die Monte-Carlo-Simulation.
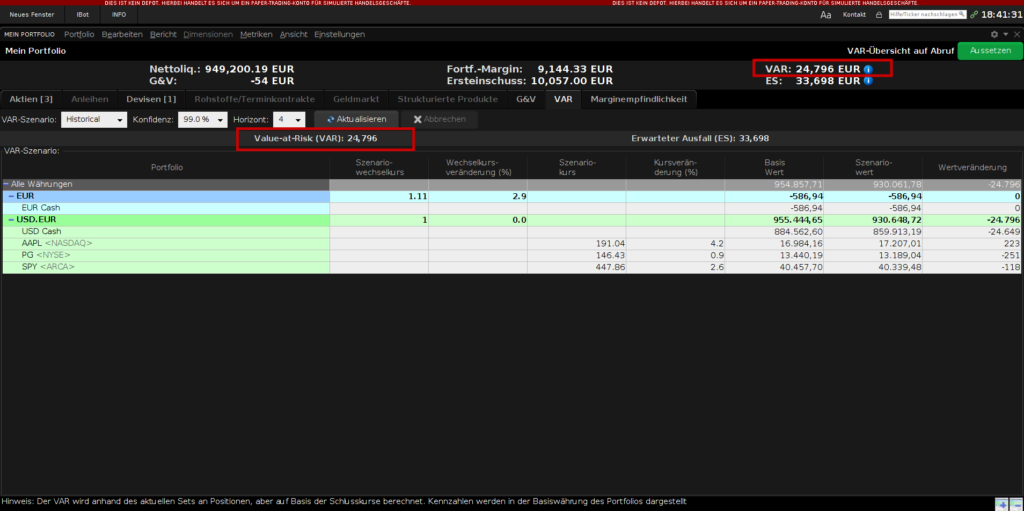
Das Konfidenzlevel lässt sich zwischen den Werten 99 %, 99,5 % und 99,9 % festlegen. Value At Risk lässt sich dann für vier verschiedene Zeithorizonte berechnen. VaR für einen Tag, eine Woche, einen Monat oder ein Jahr.
Für alle Investoren, Trader oder Anleger, die Interactive Broker nutzen, bietet die TWS somit schon das passende Werkzeug in der Handelsplattform.
Die Kritikpunkte am VaR
Wie jedes Modell ist auch der VaR nicht frei von Mängeln. Ein Hauptkritikpunkt ist, dass der VaR die Schwere der Verluste jenseits der VaR-Schwelle nicht berücksichtigt. Er gibt nur die Verlustgrenze an, die mit einem bestimmten Konfidenzlevel nicht überschritten wird. Dabei liefert VaR aber keine Informationen über die potenziellen Verluste jenseits dieses Punktes, die deutlich höher sein können. Außerdem können verschiedene Berechnungsmethoden zu unterschiedlichen VaR-Schätzungen führen, die jeweils ihre eigenen Annahmen und Einschränkungen haben. Daher sollte der VaR nicht isoliert, sondern in Verbindung mit anderen Risikobewertungsinstrumenten verwendet werden.
Fazit und Zusammenfassung
Value at Risk quantifiziert durch ein vorher festgelegtes Konfidenzlevel, die Wahrscheinlichkeit, mit der Verluste eine bestimmte Verlustschwelle nicht überschreiten. Es gibt unterschiedliche Methoden zur Berechnung des VaR, wie die Varianz-Kovarianz-Methode, historische Simulation oder die Monte-Carlo Simulation. Diese haben unterschiedliche Vor- und Nachteile, die wir hier erläutert haben. Gleichzeitig gibt es aber auch Kritik an dem Model, da die Höhe der Verluste unterhalb der Verlustschwelle nicht quantifiziert werden.
Das Modell VaR ist zwar kein Allheilmittel für alle Finanzrisiken, dafür aber ein mächtiges Instrument im Arsenal von Investoren, Tradern und Teilnehmern am Aktienmarkt. Die Fähigkeit, den potenziellen Verlust unter normalen Marktbedingungen zu quantifizieren, liefert wertvolle Erkenntnisse für das gesamte Portfolio- und Risikomanagement. Doch wie bei jedem anderen Instrument liegt auch hier die Effektivität in den Händen des Nutzers. Es ist hilfreich, die Grenzen des Modells zu kennen und es im Rahmen einer umfassenderen Risikomanagementstrategie mit Bedacht einzusetzen.