In diesem Artikel geht es um das Black-Scholes Modell (BSM) und die Berechnung des Optionspreises. Zunächst wollen wir uns anschauen, was das Black-Scholes Modell ist und wo es herkommt. Danach wird es darum gehen, wofür das Modell überhaupt genutzt werden kann. Dazu schauen uns ein paar Beispiele an. Danach folgt eine Beschreibung der Eingangsvariablen, welche das Modell nutzt und wir stellen die Black-Scholes Formeln vor. Hier folgt dann die eigentliche Berechnung. Nachdem wir das eigentliche Modell verstanden haben, zeigen wir hier ein paar Beispiele aus der Praxis. Abgerundet werden soll der Artikel dann mit den Limitierungen und Einschränkungen des Black-Scholes Optionspreismodell.
Fangen wir also mit den Grundlagen an.
Inhalt
Was ist das Black-Scholes Modell?
Bei dem Black-Scholes Modell handelt es sich um ein finanzmathematisches Modell, welches von den drei Ökonomen Fischer Black, Myron Scholes und Robert Merton entwickelt wurde, um den theoretischen Preis einer Option zu errechnen. Eigentlich müsste das Modell also Black-Scholes-Merton Modell heißen. Es ist aber überwiegend nur unter Black-Scholes Modell bekannt. Wir schreiben hier auch bewusst „theoretischer Preis der Option“, da die Preise am Optionsmarkt in der Praxis meistens von den errechneten Preisen abweichen, wie wir später noch sehen werden.
Diese drei Ökonomen veröffentlichten 1973 ein Arbeitspapier zur mathematischen Berechnung von Optionspreisen in dem Fachmagazin „Journal of Political Economy“ und erhielten dafür anschließend sogar den Nobel Preis.
Heute findet das Modell fast überall Einsatz, wo es um börsengehandelte Optionen geht. Sei es in der Finanztheorie, zum Erstellen von Modellen, in denen Optionen genutzt werden, oder in der Handelssoftware des Brokers.
Im Folgenden wollen wir uns ein paar Anwendungsbeispiele für das Black-Scholes Modell anschauen.
Wofür kann das Black-Scholes Modell genutzt werden?
Bevor wir auf die Berechnung eingehen, findest du hier ein paar Anwendungsbeispiele, die das Black-Scholes Modell in der Praxis nutzen:
- Berechnung des theoretischen Preises einer Put- oder Call-Option.
- Herleitung der „Griechen“ Delta, Gamma, Theta, Vega, Rho.
- Berechnung der impliziten Volatilität der Option.
- Die Wahrscheinlichkeit, mit der die Option am Ende der Laufzeit „im Geld liegt“ und intrinsischen Wert aufweist (In the Money).
- Die Wahrscheinlichkeit, mit der die Option am Ende der Laufzeit „aus dem Geld liegt“ (Out of the money).
- Den Break-even Preis für die Option berechnen.
- Probability of Profit (PoP) berechnen: Die Wahrscheinlich, mit der eine verkaufte (short) Option Gewinn macht.
- PoP50 für verkaufte Optionen berechnen:
Die Wahrscheinlichkeit (Probability of Profit von 50 %), dass die verkaufte Option während der Laufzeit 50 % Profit erreicht. Dies ist gerade für Stillhalter von Optionen ein wichtiger Wert. - Simulationen erstellen, mit denen sich die generelle Gewinnwahrscheinlichkeit von Optionen ausrechnen lässt.
- Berechnungen von Statistiken zu Optionen in der Handelssoftware
- uvm.
Wie du siehst, gibt es zahlreiche Anwendungsmöglichkeiten. Gerade für das Erstellen von Simulationen und umfassenderen Berechnungen rund um Optionen, sowie in jeglicher Art von Options-Handelssoftware, ist das Black-Scholes Modell nicht mehr wegzudenken.
Wie funktioniert das Black-Scholes Modell?
Nachdem wir uns jetzt einige Anwendungsbeispiele in der Praxis angeschaut haben, kommen wir zum eigentlichen Modell.
Die Grundannahmen für das BSM
Damit das Modell verlässliche Zahlen liefert, müssen einige Grundannahmen getroffen werden.
Diese sind:
- Die Optionen können erst bei Verfall ausgeübt werden. Die Zahlen aus dem Black-Scholes Modell gelten für den europäischen Optionstyp. Ein Aufschlag bei der Optionsprämie aufgrund der Möglichkeit, amerikanische Optionen jederzeit auszuüben, berücksichtigt das Modell nicht.
- Der Markt ist effizient.
- Gebühren und Provisionen für den Handel werden nicht berücksichtigt.
- Die Standardabweichung konstant und ändert sich somit während der Optionslaufzeit nicht.
Diese Annahmen sollten wir generell immer im Hinterkopf behalten, wenn wir mit dem Optionsmodell arbeiten. Weiter geht es nun mit den 5 Eingangsvariablen, die in die Berechnung einfließen.
Die 5 Variablen des Black-Scholes Modells
Der Optionspreis ist eine Funktion der folgenden 5 Variablen:
- Der aktuelle Preis des Basiswertes, hier S
- Der Ausübungspreis (Strike) der Option, hier K
- Gesamtlaufzeit der Option in Jahre, hier T
- Die jährliche (zukünftige) Standardabweichung (implizite Volatilität) des Basiswertes, hier σ (sigma).
- Der risikofreie Zins, hier r
Bevor du also die Berechnungen anstellst, benötigst du die oben genannten Daten. Kommen wir als Nächstes zu den Black-Scholes Formeln.
Die Black-Scholes Formeln
Zunächst geht es los mit der Formel zur Preisberechnung der Call-Option. Bei den folgenden Formel handelt es sich bei N() um die Verteilungsfunktion der Standardnormalverteilung. Falls du hier zu mehr lesen möchtest, habe ich hier einen guten Artikel zu verlinkt. In der Regel bieten Tabellenkalkulationen, wie Microsoft Excel oder Programmiersprachen wie Python entsprechende Tools, um N() zu bestimmen.
Preis der Call-Option
Der Preis einer Call-Option wird wie folgt berechnet:
C(S,t) = S * N(d1) - K * e^(-r*(T-t)) * N(d2)wobei
C = Preis der Call-Option
S = Preis des Basiswertes
K = Ausübungspreis (Strike) der Option
r = risikofreier Zins
N() = kumulative Verteilungsfunktion der Standardnormalverteilung
Die Variablen d1 und d2 lassen sich wie folgt berechnen:
d1 = [ln(S/K) + (r + (σ^2/2)) * T] / (σ * sqrt(T-t))
d2 = [ln(S/K) + (r - (σ^2/2)) * T] / (σ * sqrt(T-t)) = d1 - σ * sqrt(T-t)wobei
σ = Volatilität des Basiswertes in der Zukunft (implizite Volatilität der Option)
T = Gesamtlaufzeit der Option
T-t = Restlaufzeit der Option zum Zeitpunkt t
ln() = natürlicher Logarithmus
sqrt() = Wurzel (Square root)
Preis der Put-Option
Den Preis einer Put-Option berechnest du mit d1 und d2 wie folgt:
P(S,t) = K * e^(-r*(T-t)) * N(-d2) - S * N(-d1)Setzen wir nun d1 und d2 in der obrigen Formel ein und vereinfachen diese, so lässt sich noch eine andere Formel zur Berechnung des Put-Preises herleiten. Diese ist auch als Put-Call-Parität bekannt.
P(S,t) = K * e^(-r(T-t)) - S + C(S,t)Auf die Put-Call-Parität wollen wir aber in diesem Artikel nicht eingehen, da dies den Umfang sprengen würde.
Da wir jetzt die Tools zusammen haben, um die dem Black-Scholes Modell zu arbeiten, schauen wir uns jetzt ein Beispiel aus der Praxis an.
Das Black-Scholes Modell vs. Optionsmarkt
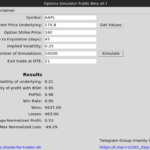
Angenommen, wir haben die folgenden Eingangsgrößen für unser Modell. Diese vergleichen wir dann mit den echten Preisen am Optionsmarkt. Dazu nutze ich die Optionskette aus der Trader Workstation von Interactive Brokers:
Basiswert: SPY
Preis des Basiswertes = 431,46 USD
Strike der Option = 415
Risikofreier Zins = 4 % (ca. der Zins der 2-jährigen US-Staatsanleihen, siehe im Market Monitor)
Laufzeit der Option = 42 Tage
implizite Volatilität der Option = 14,4 % (aus der Optionskette entnommen)
Der theoretische Preis der Put-Option
Wenn wir die oben genannten Beispieldaten in die Formeln eintragen, erhalten wir einen theoretischen Preis der Put Option mit dem Black-Scholes Modell von 2.14 USD.
Am Optionsmarkt ist der Preis ein etwas anderer. Nicht viel, aber dennoch wichtig zu verstehen.
Der Marktpreis der Put Option
Wie wir am folgenden Screenshot aus der TWS sehen, wird die oben ausgerechnete Put Option für 2.38 USD gehandelt. Also über 10 % höher, als theoretische Preis aus dem Modell.
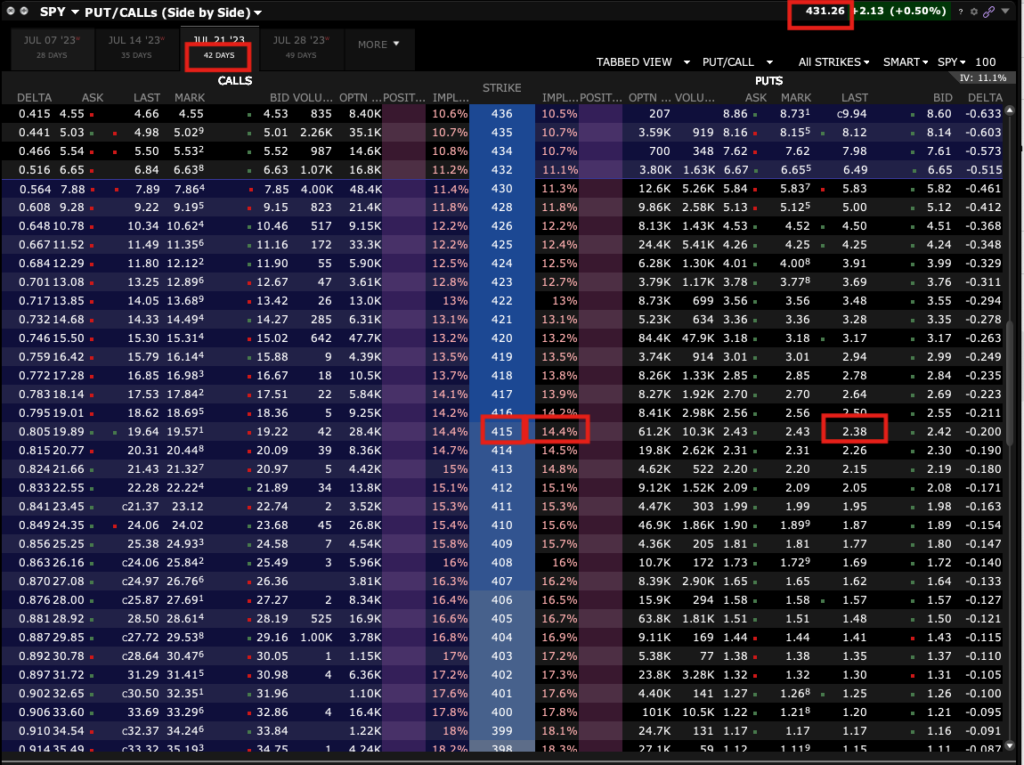
Trotzdem bietet das Modell eine gute Näherung zu dem gehandelten Optionspreis. Wir haben oben ja bereits über die Grundannahmen des Modells gesprochen. Eine der Annahmen war die Gültigkeit nur für europäische Optionstypen, die erst nach Verfall ausgeübt werden können. Bei den Optionen auf den SPY ETF handelt es sich um Optionen des amerikanischen Typs. Daher könnte der Preisaufschlag durch die Möglichkeit des Rechts einer früheren Ausübung zustande kommen. Des Weiteren lässt die risikofreie Rendite auch etwas Interpretationsspielraum, auch wenn diese nur zu einem geringen Bruchteil Einfluss auf die Berechnung hat.
Limitierungen und Einschränkungen des Black-Scholes Modell
Wie wir gesehen haben, bietet das Black-Scholes Modell eine sehr gute Annäherung an den echten Optionspreis und bietet so ein unersetzliches Tool für weitere Modelle rund um den Optionshandel.
Trotzdem hat das Modell einige Einschränkungen, die es zu beachten gilt.
Die Volatilität des Basiswertes ist in der Realität nicht konstant
Das Optionspreismodell geht davon aus, dass die Volatilität des Basiswertes über die Laufzeit der Option konstant ist. Gerade für diejenigen Optionshändler, die Volatilität verkaufen, ist das ein wichtiger Punkt. Bei Aktien führen zum Beispiel der Zeitpunkt von Earnings (Gewinnmitteilungen) oft zu einem Zusammenbruch der impliziten Volatilität der Option, da das Ereignis „Earnings“, eine Unsicherheit vom Markt nimmt. Dies gilt dann entsprechend bei der Modellierung und Verwendung des Black-Scholes Models zu berücksichtigen.
Der theoretische liegt in der Regel über dem realen Optionspreis
Wie wir an unserer Beispielrechnung gesehen haben, liegt der gehandelte Optionspreis üblicherweise über dem theoretischen und berechneten Preis. Es lässt sich mit dem Modell somit nie der exakte Preis berechnen. Trotzdem reicht die Genauigkeit der BSM, um dieses in weiteren Modellen zu nutzen.
Dividenden werden nicht berücksichtigt
Das Black-Scholes Model berücksichtigt nicht den Einfluss von Dividendenzahlungen. Schüttet ein Unternehmen Dividenden aus, so führt dies zu einer Abwertung des Aktienkurses, da Kapital das Unternehmen verlässt. Dies wird im BSM nicht berücksichtigt. Kann aber recht einfach durch einen Abschlag beim Kurs des Basiswertes im Modell korrigiert werden.
Es gilt nur für Optionen europäischer Art
Da das Modell nur für Optionen gilt, die erst nach Verfall ausgeübt werden können, wird dies nicht mit eingepreist. Das Recht, jederzeit die Option ausüben zu können, sollte theoretisch einen kleinen Preisaufschlag bedeuten. In der Praxis sieht es aber so aus, dass Optionen nur ausgeübt werden, wenn sie entweder tief im Geld sind (Strike der Put-Option >> Preis des Basiswert) oder die Option im Geld ist und die Option nur noch wenige Tage (bis 2-3 Wochen) bis zum Verfall läuft. Denn nur dann macht es für den Besitzer der Option auch finanziell Sinn, diese auszuüben.
Fazit und Zusammenfassung
In diesem Artikel haben wir uns intensiv mit dem Black-Scholes Modell zur Bepreisung von Optionen auseinandergesetzt. Wir haben uns angeschaut, wo das Modell seinen Ursprung hat und was für Anwendungsfälle es gibt. Danach sind wir zur Berechnung übergegangen, haben die Grundannahmen und Inputgrößen für das Modell gesprochen und uns ein Praxisbeispiel angeschaut. Zuletzt sind wir auf einige Einschränkungen des Modells eingegangen.
Zusammenfassend lässt sich sagen, dass dieses Modell von der Welt mit Optionshandel nicht mehr wegzudenken ist. Während die meistens Handelsplattformen so gut wie alle Optionsparameter berechnen, können mithilfe des BSMs weitere umfassendere Modell zu Optionen im Allgemeinen erstellt werden.
So zum Beispiel ein Modell für die Berechnung der Gewinnwahrscheinlichkeit PoP (Probability of Profit) oder der 50% Gewinnwahrscheinlichkeit für alle Stillhalter und Optionsverkäufer (PoP50).