Alles was du über das Vega einer Option wissen musst
Bei Vega handelt es sich neben Delta, Gamma und Theta um einen weiteren Optionsgriechen, der aus dem Black-Scholes-Model abgeleitet ist. Mit dem Optionsgriechen lassen sich Optionen in ihren Eigenschaften mathematisch beschreiben. Vega beschreibt den Einfluss der Volatilität auf den Optionspreis.
In einem Satz lässt sich Vega wie folgt zusammenfassen:
Vega gibt an, um welchen Betrag sich der Preis der Option ändert, wenn sich die Volatilität um 1% ändert.
Inhalt
Mathematische Definition von Vega gemäß Black-Scholes-Modell
Vega zählt zu den Optionsgriechen, auch wenn es sich bei Vega diesmal nicht um einen griechischen Buchstaben handelt. Mathematisch gesehen lässt sich Vega, abgeleitet aus dem Black-Scholes-Modell, wie folgt ausdrücken:
$$vega=\frac{\delta V}{\delta \sigma}$$
Bei $\delta V$ handelt es sich um die Änderung des Optionspreises und bei $\delta \sigma$ um die Änderung der impliziten Volatilität der Option. Bei $V$ kann es sich um den Preis einer Put oder Call Option handeln.
Aus dem Black-Scholes-Modell lässt sich folgende Gleichung ableiten, um Vega zu berechnen.
$$vega = S\phi(d_1)\sqrt{T}e^{-rt}$$
In der Gleichung handelt es sich bei $S$ um den Preis des Basiswerts, bei $\phi(d_1)$ um die Dichtefunktion der Wahrscheinlichkeit bei $d_1$. Bei $T$ handelt es sich um die Zeit bis zum Verfall der Option in Jahren und bei $r$ um den risikofreien Zinssatz während der Laufzeit der Option. Hinter dem $d_1$ der Wahrscheinlichkeitsdichtefunktion $\phi$ steckt eine weitere komplexere Formel:
$$d_1 = \frac{ln\left(\frac{S}{K}\right)+(r+\frac{\sigma²}{2})T}{\sigma\sqrt{T}}$$
Bei K handelt es sich um den Strike der Option.
Um die Funktionsweise von Vega beim Optionshandel zu verstehen, brauchen wir jedoch nicht in die Tiefen der Mathematik einzutauchen. Uns reicht grundsätzlich die oben beschriebene Kurzformel, sowie ein Blick auf die Ergebnisse, die aus dieser Formel und dem Black-Scholes-Modell resultieren.
Der Einfluss von Vega auf den Gewinn und Verlust
Wir stellen die vereinfachte Formel für Vega nach der Änderung des Optionspreises $\delta V$ um. Diese sieht dann wie folgt aus:
$$\delta V = vega * \delta \sigma$$
Aus dieser einfachen Formel können wir nun folgende Erkenntnisse ziehen:
- Ist Vega positiv, so führt eine Vergrößerung der impliziten Volatilität zu einem höheren Optionspreis.
- Ist Vega negativ, so führt eine Vergrößerung der impliziten Volatilität zu niedrigerem Optionspreis.
Als Optionstrader wissen wir, dass Optionen mit dem Anstieg der IV (impliziten Volatilität) teurer werden. Auf der anderen Seite werden diese günstiger, wenn die IV abnimmt.
Also können wir schlussfolgern:
- Vega ist positiv für Long Optionen (Optionskäufer)
- Vega ist negativ für Short Optionen (Optionsverkäufer / Stillhalter)
Dies ergibt intuitiv Sinn, denn bei einem Abfall der Volatilität verdienen Stillhalter Geld mit Short Optionen während Käufer von Lotterietickets (Long Optionen) Geld verlieren.
Vega einer Long und Short Option mit Zahlenbeispiel
Für Zahlenbeispiele greifen wir wieder auf folgende Gleichung zurück
$$\delta V = vega * \delta \sigma$$
$\delta V$ ist wieder die Änderung des Optionspreises und $\delta \sigma$ die Änderung der Volatilität.
Zahlenbeispiel für das Vega einer Long Option
Angenommen, wir kaufen eine Aktienoption für 1 USD. Beim Kauf der Option zahlen wir also 100 USD. Zum Zeitpunkt des Kaufs hat die Option ein Vega von 0,08. Der Markt wird nervöser und die implizite Volatilität der Option erhöht sich um 3 %. Wie ist nun unser Gewinn- und Verlust?
Hier unserer Eingangsgrößen für die Formel:
- Bezahlte Prämie für die Put-Option = 100 USD
- Vega = 0,08 USD
- $\delta \sigma$ = 3 %
Diese Werte setzen wir jetzt in die oben beschriebene Formel und erhalten:
$$\delta V = 0,08 * 3 = 0,24$$
Da wir in der Option Long sind, beträgt unser Gewinn jetzt 24 USD.
Hätte die Volatilität auf der anderen Seite um 3 % abgenommen, wäre die Volatilitätsänderung negativ ($\delta \sigma$ = -3 %). Damit verliert unsere Position dann 24 USD an Wert.
Zahlenbeispiel für das Vega einer Short Option
Wir verkaufen eine Option für 1,50 USD mit einem Vega von -0,15. Damit sind wir Short in der Option. Mit dem Verkauf der Option vereinnahmen wir sofort die Prämie von 150 USD. Beim Verkauf dieser Option ist die Volatilität überdurchschnittlich hoch und der IVR liegt bei 55. Am nächsten Tag ist die Volatilität der Option bereits um 5 % gesunken.
Wie hoch ist nun der Gewinn der Position in unserem Portfolio?
Wir setzen die Zahlen nun in unsere Formel ein:
- Vereinnahmte Optionsprämie = 150 USD
- Vega = -0,15 USD
- $\delta \sigma$ = -5%
Wie setzen ein:
$$\delta V = (-0,15) * (-5) = 0,75$$
Unsere Position mit der Short Option gewinnt jetzt 75 USD an Wert. Die Option ist um 75 USD günstiger geworden. Als Optionsverkäufer bzw. Stillhalter wollen wir die Option günstiger zurückkaufen bzw. verfallen lassen.
Würde die implizite Volatilität um 5 % ansteigen anstatt zu fallen, so würde sich die Option um 75 USD verteuern. $\delta V$ würde negativ und wir säßen auf einem Buchverlust von 75 USD.
Der Einfluss von Delta auf Vega (kurze Laufzeit, niedrige Volatilität)
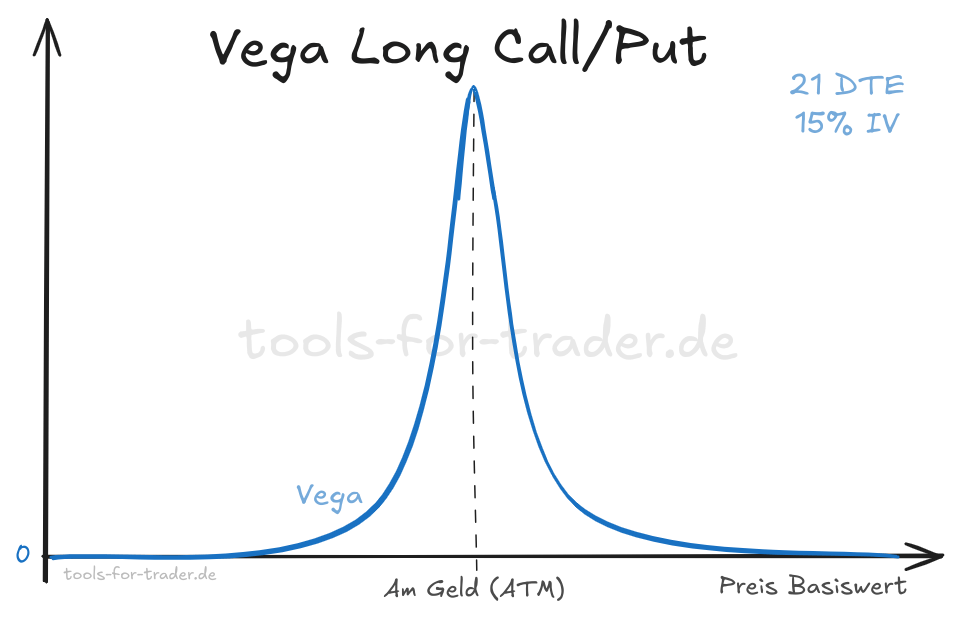
Wir plotten Vega anhand der Vegaformel aus dem Black-Scholes-Modell. Als Parameter nutzen wir eine Option mit 21 Tagen Restlaufzeit und einer konstanten impliziten Volatilität von 15 % über alle Strikes. Damit ergibt sich dann folgendes Bild.
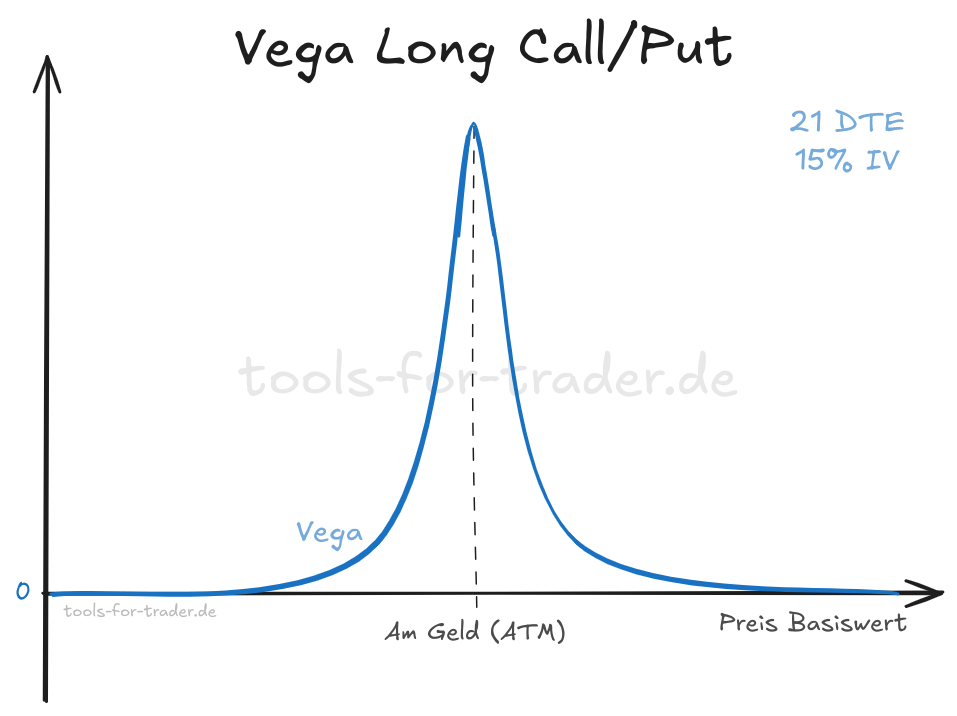
Wir sehen, dass Vega hier für Optionen am Geld (ATM) am höchsten ist. Hier hat eine Änderung der impliziten Volatilität den größten Einfluss auf den Preis der Option. So kann der Preis der Option bei einem Anstieg der impliziten Volatilität der Option dann schnell nach oben schießen. Auf der anderen Seite aber auch wieder schnell abfallen.
Gehen wir mit der Option weiter aus dem Geld oder ins Geld, so fällt Vega und damit der Einfluss der Volatilität auf den Optionspreis stark ab. Eine aus dem Geld bzw. tief im Geld liegende Option hat dann kaum bzw. kein Vega mehr.
Dies gilt speziell für kurz laufende Optionen und bei niedriger impliziter Volatilität. Hier am Beispiel für eine Option mit 21 Tagen Laufzeit (DTE) und 15 % implizite Volatilität (IV).
Der Einfluss der Restlaufzeit (DTE) der Option auf Vega
Betrachten wir nun eine Option mit 45 Tagen Laufzeit (DTE) und konstanter 15 % IV (Implizite Volatilität), so sehen wir einen deutlichen Anstieg von Vega über alle Preise des Basiswerts.
Mit höherer Laufzeit wird also auch Vega größer.
$$vega = S\phi(d_1)\sqrt{T}e^{-rt}$$
Ein Blick auf die Formel für Vega zeigt, wie die Restlaufzeit $T$ in der Multiplikation zu Vega beiträgt.
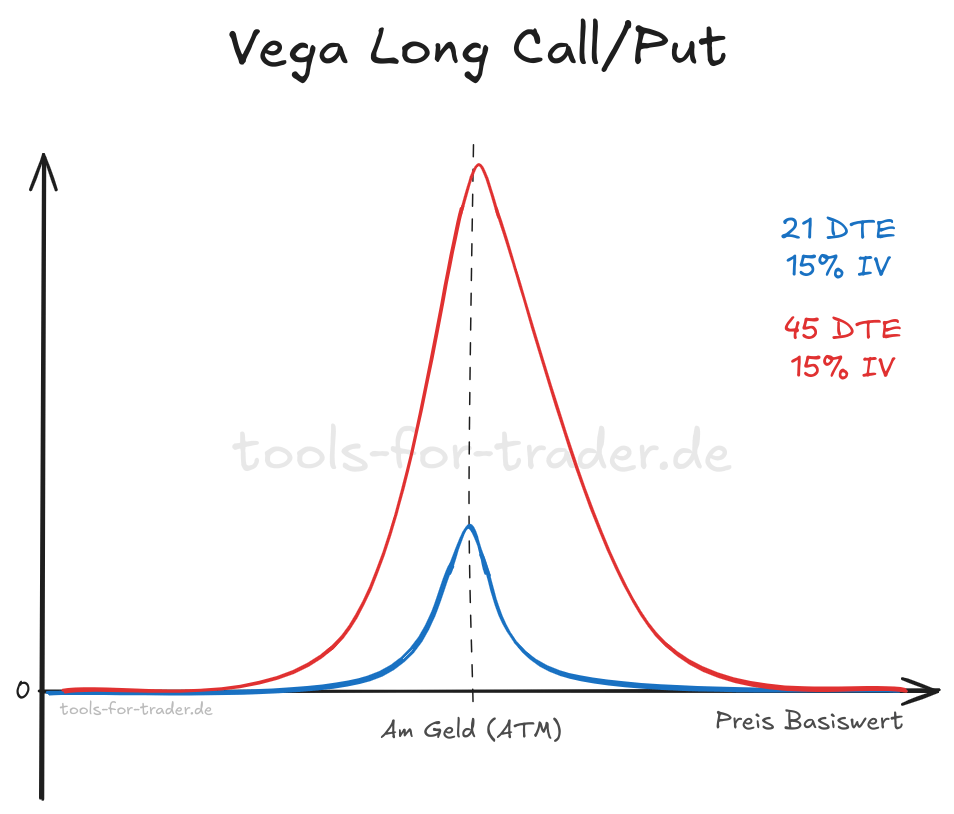
Gleichzeitig verschiebt sich das Maximum von Vega leicht nach rechts weg vom Preis Basiswertpreises, welcher am Geld liegt.
Wir können also festhalten:
- Je länger die Laufzeit der Option, desto größer ist Vega. Einfluss der Volatilitätsänderung auf den Optionspreis wird größer.
- Je kürzer die Laufzeit der Option, desto kleiner ist Vega. Der Einfluss der Volatilitätsänderung auf den Optionspreis wird kleiner.
Der Einfluss der impliziten Volatilität der Option auf Vega
Die implizite Volatilität (IV) hat einen großen Einfluss auf das Vega der Option. Wir haben gezeigt, dass mit längerer Laufzeit Vega größer und mit kürzerer Laufzeit kleiner wird.
Was passiert nun mit Vega bei höherer Volatilität?
Dazu schauen wir uns wieder an, wie Vega der Option über den Preis des Basiswerts verläuft. Diesmal erhöhen wir die Volatilität auf 30 % und erstellen den neuen Graphen in Grün mit konstanter 30 % IV und 45 DTE neben den schon bekannten.
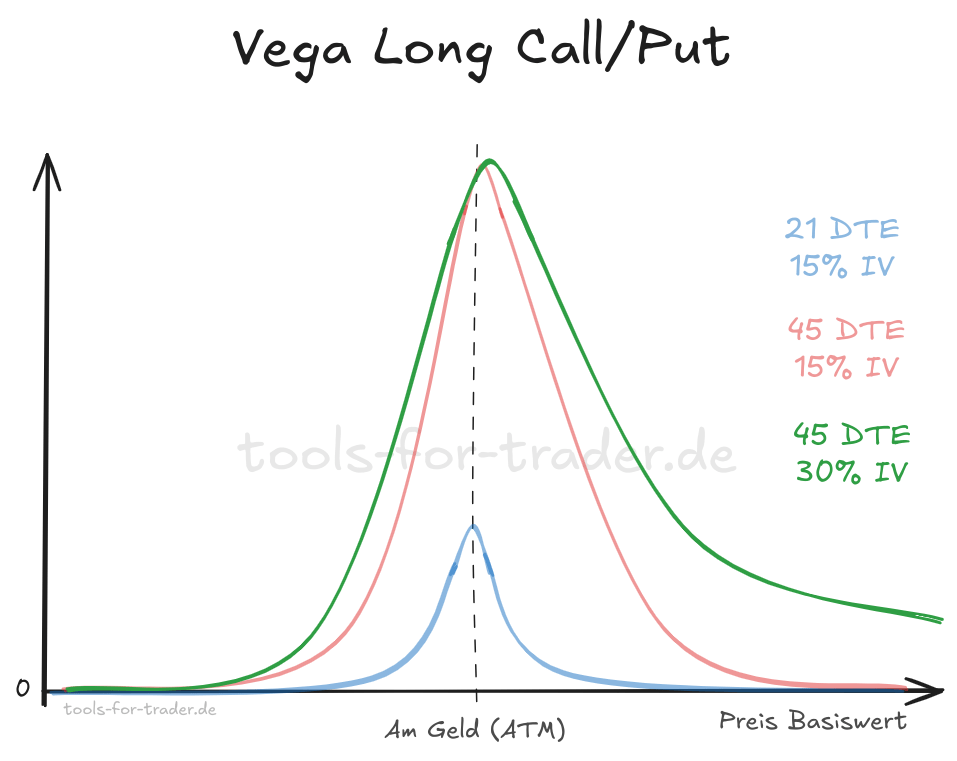
Der maximale Betrag von Vega verändert sich durch die höhere Volatilität nicht. Wir sehen jedoch, dass der Verlauf von Vega sich breiter nach links und rechts über die Preise des Basiswerts verteilt. Je höher die implizite Volatilität, desto weiter verschiebt sich das Maximum von Vega nach rechts weg vom Geld. Außerdem fällt Vega mit höher Basiswertpreisen flacher ab.
Einsatz von Vega beim praktischen Optionshandel
Zum Schluss noch einige Ansätze für die Verwendung von Vega beim Optionshandel. Speziell auch für Stillhalter.
Vega als Shortseller (Stillhalter) für sich arbeiten lassen
Als Verkäufer einer Option (Stillhalter) können profitieren wir nicht nur vom Zeitwertverfall Theta, sondern auch von einem Zusammenbruch der Volatilität. Mit einer Short Option platzieren wir uns also nicht nur Long Theta, sondern auch Short Vega und setzen damit auf einen Zusammenbruch der Volatilität.
Aus diversen Studien und Backtests, zum Beispiel von Tastylive, wissen wir, dass Volatilität sich langfristig immer wieder zum Mittelwert bewegt. Verkaufen wir Optionen bei relativen hohen impliziten Volatilitätslevels, profitieren wir von diesem Verfall der Volatilität. Die relative implizite Volatilität eines Basiswerts lässt sich mit dem IVR (Impliziten Volatilität Rang) oder IVP (Implizites Volatilität Perzentil) bestimmen. Suchen wir für den Verkauf von Optionen bewusst Basiswerte mit relativen hohen IVs und platzieren uns Short Vega, profitieren wir zweimal. 1. vom Zeitwertverfall Theta und 2. vom Zusammenbruch der Volatilität.
Genau wie der Zeitwertverfall lässt ein Abfall der Volatilität den Optionspreis fallen, sodass wir die Option im Idealfall günstiger zurückkaufen oder verfallen lassen können.
Vega arbeitet heimlich im Hintergrund – Delta und Theta bleibt King
Bei Vega handelt es sich um einen der Optionsgriechen, der heimlich im Hintergrund arbeit. Vega ist nicht so präsent und transparent wie Delta oder Theta. Delta und Theta sind für uns Optionshändler immer da und immer präsent. Vega ist eher versteckt und wir als Stillhalter merken eine Änderung der Volatilität im gesamten Short Optionsportfolio.
Für den täglichen Optionshandel reicht ein solides Grundverständnis von Vega. Mit mit dem täglichen Blick auf das Porftolio-Delta und Portfolio-Theta und dessen Adjustierung lässt sich das effektivste Risikomanagement der offenen Positionen betreiben. In der TWS von Interactive Brokers (Affililink hier) lässt sich auch das Portfolio-Vega anzeigen. Hiermit bekommen wir eine Indikation, wie sich der Gewinn- und Verlust des Portfolios ändert, wenn Sie die Volatilität im Markt (VIX) verändert. Jedoch lässt sich auf dieser Basis als Stillhalter das Portfolio mit Vega nicht sinnvoll managen.
Hedging von Vega ist nur mit Long Optionen möglich. Entweder ist die Volatilität erhöht und unsere Strategie verfolgt eine Short Vega Strategie (Stillhalter), oder wir kaufen Optionen und sind damit Long Vega. Für letzteres sollte die Volatilität sehr niedrig sein, so dass ein Anstieg der IV wahrscheinlich ist.